1.1 结构模型

依据实际中常规的除尘器壳体结构几何参数，设计了10例基础研究模型，几何参数如表1所示。这些模型涵盖了大型、中型、小型除尘器的几何尺寸，确保研究结果具有普遍性。实际除尘器一般布置有多跨围护墙板，以保证收尘效果。为简化模型，提高计算效率，仅取两跨墙板建模。中间双肢组合柱截面如图1(b)所示。H型钢柱与墙板直接相连的一侧翼缘称为后翼缘，不受墙板约束的立柱翼缘称为前翼缘。连接墙板与两肢立柱的腹板通过焊接连接。立柱总高度H，横向支撑间距l0 (即连接槽钢间距，亦为单肢立柱绕y轴的计算长度)，壳体墙板宽度w，连接墙板宽度b，墙板与连接墙板壁厚t，连接墙板中心与后翼缘距离y2。

1.2 有限元计算模型

采用ANSYS有限元程序进行数值分析，选用Shell181单元对所有结构构件进行模拟。材料参数如表2所示。钢材本构采用双线性等向强化模型，以米赛斯准则判断是否发生屈服。考虑几何非线性影响，采用弧长法跟踪结构响应路径。

表1 计算模型几何参数

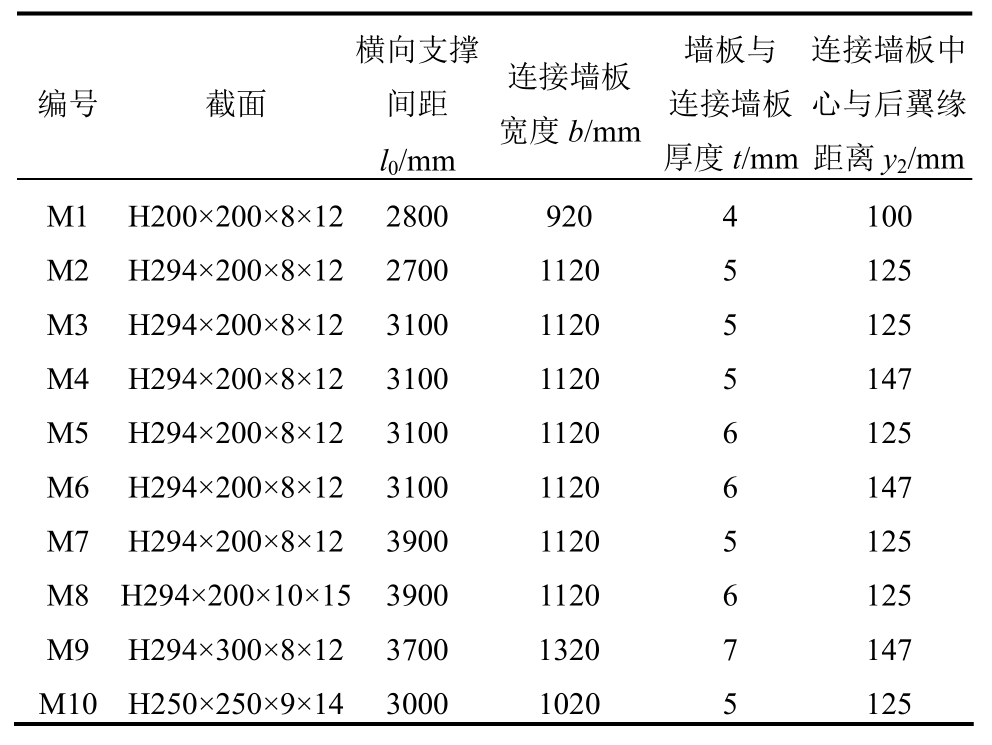
Table 1 Geometrical parameters of computational models

表2 结构材料参数

Table 2 Material parameters of the structure

根据实际情况，对有限元模型施加约束与荷载。对于壳体墙板，在顶部与底部施加垂直于墙板方向的平动约束(y向)，模拟大刚度加劲顶板、灰斗加劲壁板的约束。对于壳体立柱，在两肢间连接槽钢中点位置施加垂直墙板方向的平动约束(y向)，模拟等间距布置横向支撑的约束;在中柱底部施加3个方向的平动约束;在两侧边柱底部仅施加垂直于墙板方向和高度方向的平动约束(y和z向)，以释放高温烟气产生的墙板平面内温度变形;在中间组合柱顶设置一块刚性盖板，便于施加竖向均布荷载。

1.3 有限元分析方法验证

为验证本文中有限元建模、加载和求解方法的准确性，对文献[11]中双向加劲钢板在轴向和横向荷载共同作用下破坏性加载试验进行非线性有限元模拟。根据文献中记载的试验模型几何尺寸和约束情况建立有限元验证模型，钢材材性采用论文中给出的实测数据的平均值。加载试验中轴向荷载加载速率较快，并较早达到预定值，横向荷载加载速率较慢，最后破坏是在横向荷载作用阶段。因此，按照实际试验加载过程，有限元模拟中首先施加轴向荷载，其次施加横向荷载至破坏。本文模拟得到的极限承载力与文献中试验结果对比如表3所示;两个典型模型加劲板中心结点荷载-位移曲线的有限元模拟情况与试验记录情况对比分别如图2(a)和图2(b)所示。可见，有限元模拟结果与试验结果在极限承载力与荷载-位移响应路径方面吻合良好，本文有限元模型构建方法与非线性分析技术基本可靠，能满足后续结构体系承载性能研究的要求。

表3 本文有限元结果与文献试验结果对比

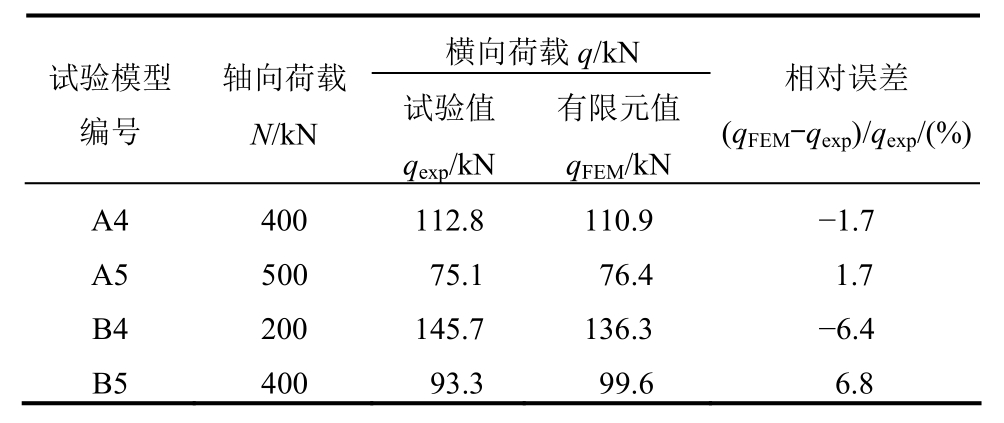
Table 3 Comparison of results between finite element method and tests

图2 荷载-位移曲线的有限元模拟情况与试验记录情况对比

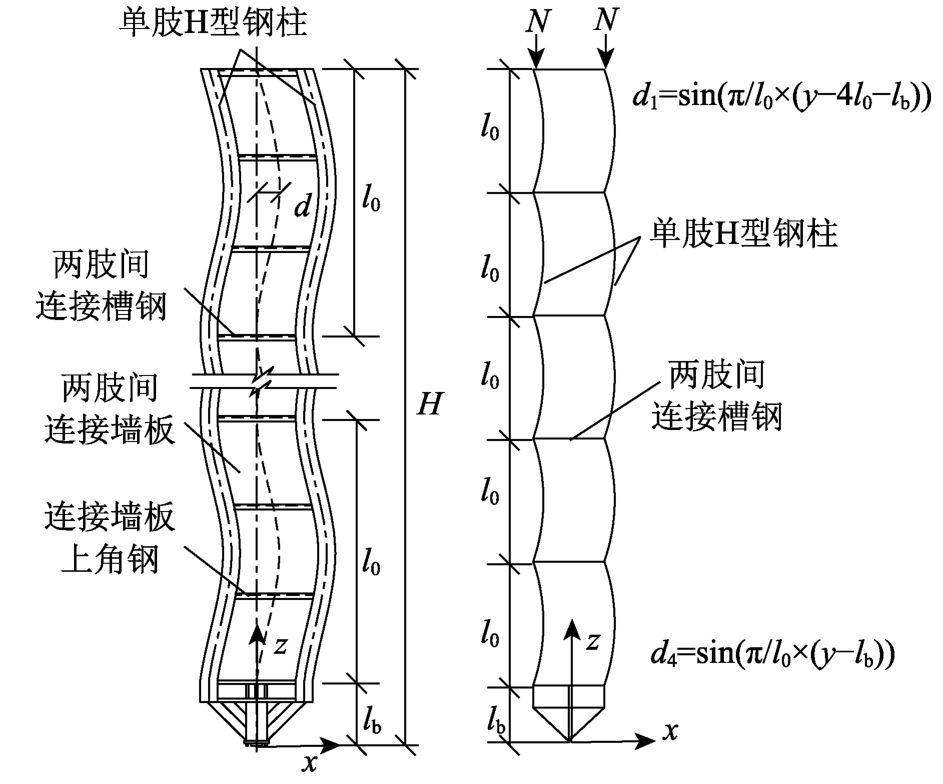
Fig.2 Comparison of the load-displacement curves between finite element simulations and test records

1.4 初始几何缺陷

文献[12]中对除尘器壳体结构体系中单肢H型钢柱轴压稳定性的敏感初始几何缺陷进行了研究，结果表明，柱顶区域前半截面(前翼缘与前腹板)的弯扭变形对单肢H型钢柱稳定性是最不利的。这是因为墙板作为蒙皮结构，能够为立柱承担荷载，导致仅在靠近柱顶的局部区域存在高压应力;且墙板的存在增大了后翼缘受载面积，使得其荷载水平低于前翼缘;前翼缘相对较自由，容易发生变形。双肢柱的内力分布、变形约束与单肢H型钢柱类似，因此这种最不利初始缺陷同样适用于本文的双肢组合截面柱。

基于这样的推断，建模时首先对中间两肢H型钢柱在各连接槽钢区间(连接槽钢可视作H型钢柱的侧向支撑)构造了绕y轴的正弦半波形式初始几何缺陷，形成初始弯曲变形，缺陷形式如图3所示。缺陷幅值δ取千分之一柱高。

为了引入前半部分截面的初始扭转变形，并考虑墙板及连接墙板上初始几何缺陷的影响，对仅有立柱正弦半波整体缺陷的结构模型施加柱顶轴力进行非线性计算，同时对立柱一侧翼缘施加均布扰动线荷载qd。扰动荷载作用范围为立柱上轴压应力由σz,max(最大轴压应力)衰减到0.85σz,max的区间，扰动荷载合力值取柱顶轴向荷载的千分之一，扰动荷载的施加如图1(b)所示。达到荷载极值点时结构上较大的变形为连接墙板靠近柱顶区域和中上部墙板邻近立柱区域的y向变形，立柱的变形幅值与之相比不超过15%。将此模型达到极值点时的变形模态作为结构极值点变形缺陷模态，幅值取千分之一柱高。后续分析均引入这种几何缺陷模态。这样的缺陷模型既包括了立柱在高压应力区易于变形的前半部分截面初始弯扭变形，又包括了墙板和连接墙板上的局部凹凸变形，充分考虑了最不利初始几何缺陷的影响。

图3 初始弯曲缺陷形式

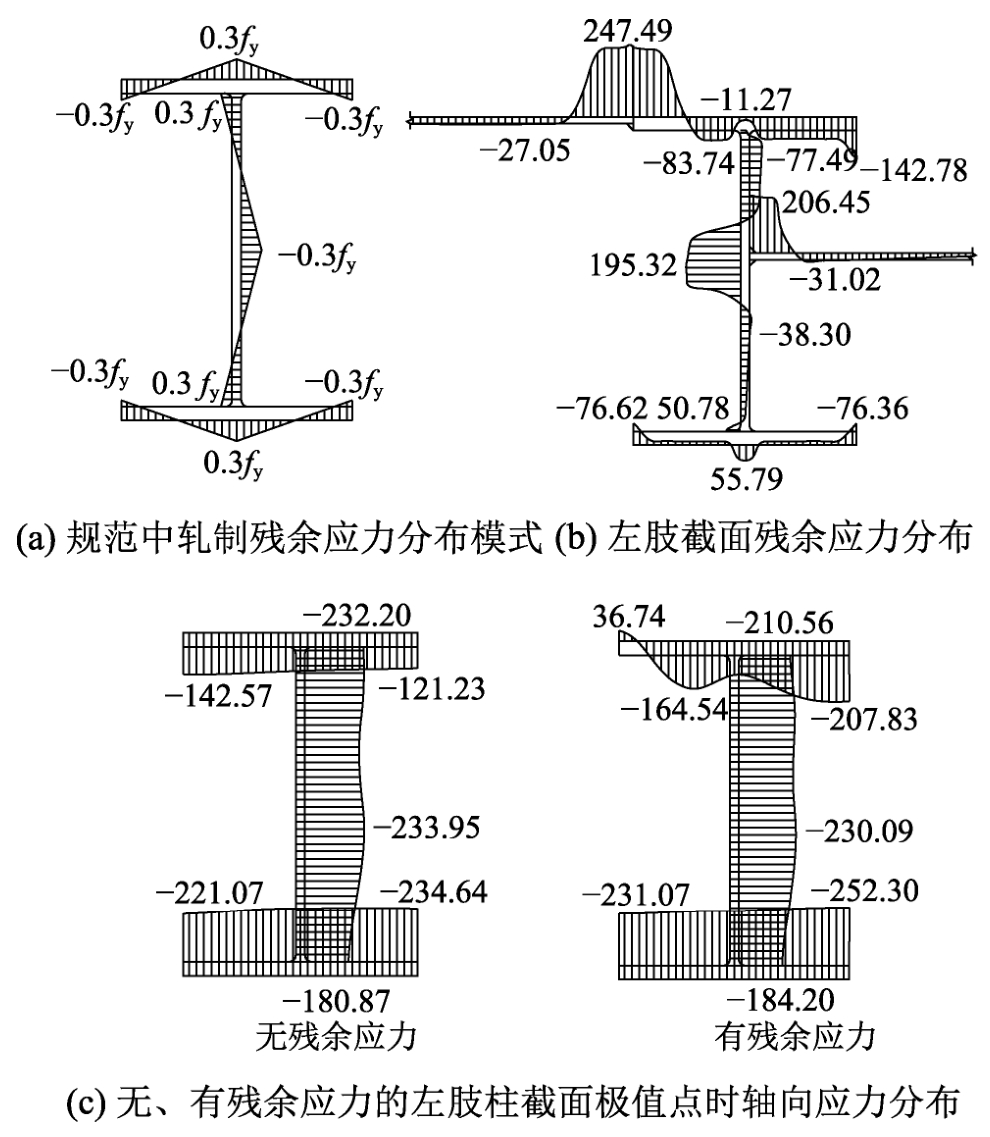
Fig.3 Initial bending imperfection shape of the column

1.5 焊接残余应力的影响

结构体系中残余应力的形成源于3个步骤：一是H型钢的轧制过程;二是H型钢腹板与连接墙板的焊接过程;三是H型钢后翼缘与墙板的焊接过程。残余应力的存在会影响立柱的稳定性。本文通过有限元方法，利用瞬态移动热源和生死单元技术模拟焊接过程中的温度场变化，通过热力耦合将瞬时温度作为外荷载施加到实体结构上，形成应力场。对于热轧H型钢的轧制残余应力，我国钢结构规范采用图4(a)的模式[13]。因此模拟轧制过程时，控制H型钢各板件残余拉、压应力幅值为0.3fy，即70.5MPa左右。钢材高温下力学材料性能(弹性模量E与屈服强度fy折减系数)、热学材料性能(导热系数λ、热膨胀系数α、比热容C)均按照《建筑钢结构防火技术规范》[14]取值。为简化计算，忽略辐射的影响，仅考虑对流换热。换热系数取15W·m-2·℃-1。以模型M5为例，考虑对称性，左肢H型钢最终形成的轴向残余应力分布如图4(b)所示。图4(b)表明，H型钢腹板与连接墙板连接处、H型钢后翼缘与墙板连接处由于焊接过程中温度较高冷却较慢而产生较大的残余拉应力，其中，后翼缘与墙板连接处由于焊接次序最末，产生的残余拉应力最大，可达屈服强度fy。残余拉应力自焊接部位向外衰减较快。H型钢前翼缘最终残余应力分布情况受轧制的影响较大，前翼缘与腹板连接处产生残余拉应力，其余部位产生残余压应力。焊接过程增大了前翼缘的残余压应力，但改变幅度很小，不超过0.03fy。

图4 残余应力与荷载极值时轴向应力分布图 /MPa

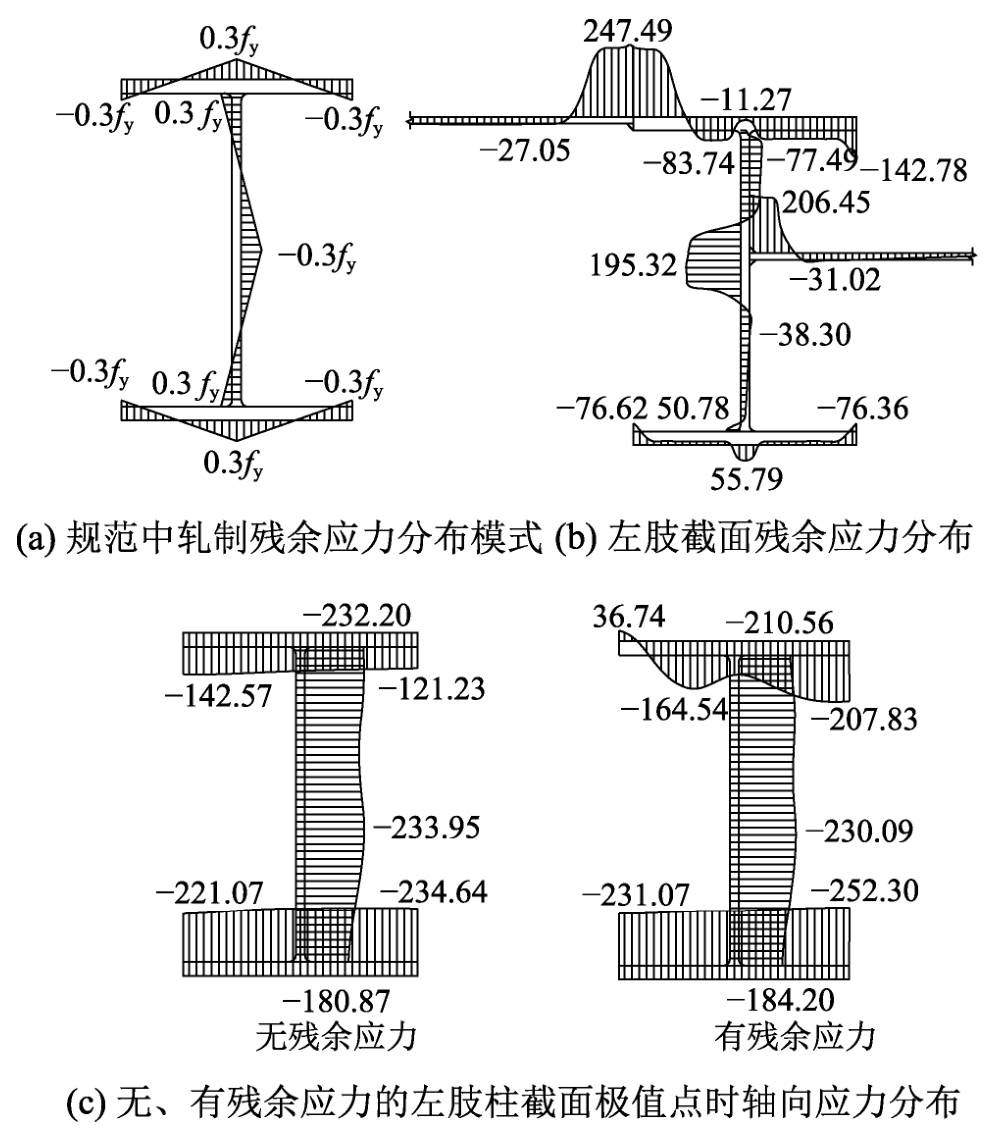
Fig.4 Distributions of residual stress and axial stress at load extremes

为考察残余应力对立柱轴压承载能力的定量影响，将利用实体单元进行轧制与焊接过程模拟形成的残余应力分布简化后引入壳单元构建的结构体系有限元模型进行非线性计算，计算结构在有、无残余应力时的稳定承载力。对于不同构造与尺寸的模型M1和M5，考虑残余应力后的稳定承载力分别为未考虑残余应力的0.971倍与0.989倍，减小幅度均不超过5%。同一截面上，无、有残余应力情况左肢立柱截面达到极限承载力时的轴向应力分布如图4(c)所示。立柱的失稳主要体现为前半部分截面的失稳，在无残余应力情况荷载达到极值时，腹板与前翼缘组成截面的压应力分布较为均匀，基本接近全截面屈服的水平。残余压应力的存在可能会透支一定前半部分截面应力增加空间，但图4(b)表明，多步加工使得前腹板与前翼缘上的残余拉、压应力分布基本平衡，残余应力引起初始轴向内力合量不超过该部分截面屈服荷载的5%。图4(c)表明，有、无残余应力情况最终发生破坏时的立柱截面轴向应力分布差异不大，有残余应力时前翼缘的压应力水平更高一些。在有、无残余应力时，分别对H型钢前半部分截面轴向加载阶段计算应力增量积分(即前半部分截面的轴向内力加载量)，继而求出比值，M1模型有、无残余应力情况轴力增量比值为0.983，M5模型有、无残余应力情况轴力增量比值为0.982。可见，由于易于发生失稳的H型钢前半部分截面残余应力基本平衡，且达到极限承载力时截面处在一个较为均匀的高压应力水平，因此残余应力的影响不大。考虑到由于残余应力的存在立柱承载力减小幅度不超过5%，且这种影响对于不同构造立柱差异不大，因此，为简化计算，后续有限元模型中不再引入残余应力，而用一个偏于安全的折减系数来反映残余应力的不利影响。